A Fast and Simple Asynchronous ADC

      (Auto-Folding Multi-Bit Comparator)

              (US Pat. 7839317)

This invention could have been invented in the late 60's.

Would a high speed comparator which provides a multi-bit output been 

useful back then? And the architecture is simple and all NPN.

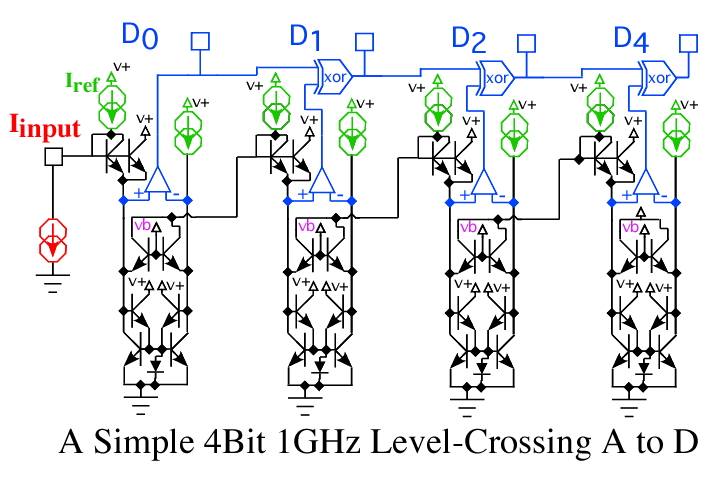
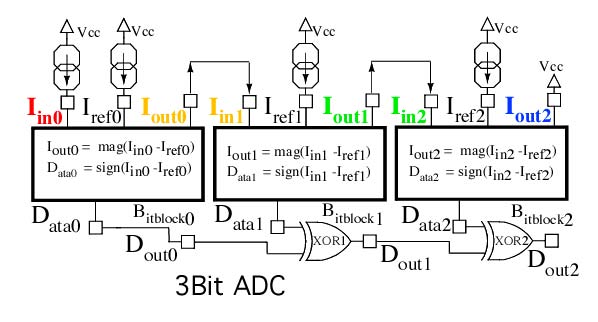
The circuit shown above is actually the full schematic for a 4 bit 1GHz

asynchronous level crossing A to D. The digital elements shown in 

blue are not drawn at transistor level since differential logic

needs to be used. All the DC reference currents shown in green 

match each other in current value. All NPNs are minimum 1X geometries, 

and the reference currents are chosen to run all NPNs at their

maximum ftau. The analog input shown in red is an input current having

a full scale range from zero to the reference current level. 

When the NPNs are modeled as having a ftau at 4GHz, the digital output

response to a full scale 16ns ramp input current is shown below. 

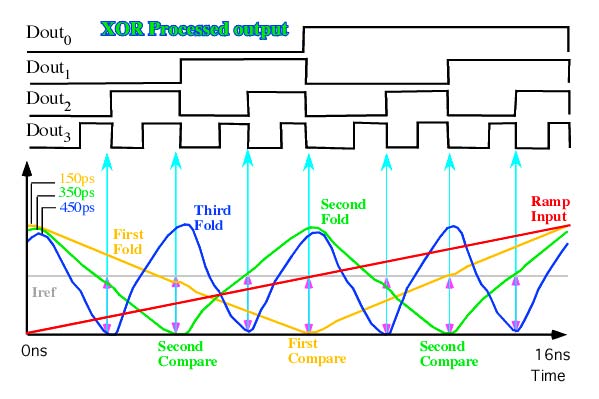
Each cell is doing a current comparison to the reference current,

but it is also outputting a folded version of the analog signal current

as well. Some simple first order speed up techniques have been applied

to allow 4GHz NPNs to track a moving input with no missing

codes at a 1GHz rate. Some much better modeling, and some more advanced 

speed up techniques might allow the LSB tracking output code rate to come 

even closer to the ftau of the transistors. 

The XOR logic circuit is reformatting the digital output into

the normal binary format. Notice how when the MSB reverses state,

all the other bits need to reverse state at the same time. 

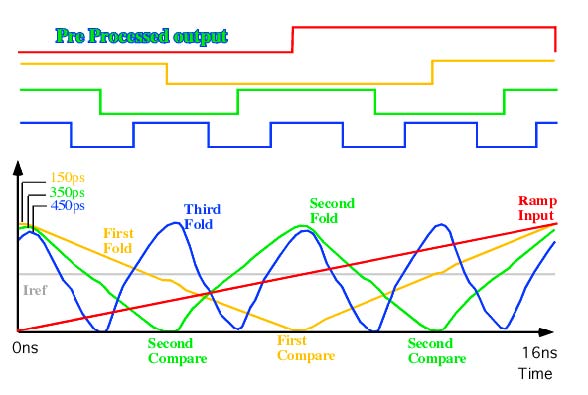
The pre-processed digital output has an interesting format.

Only one cell is able to switch state at a given time. 

When any of the cells switch state, all the other

cells are stationary.  So a single output state change

could trigger all the bits to be cleanly sampled. The 

XOR function can then be applied later at any time. 

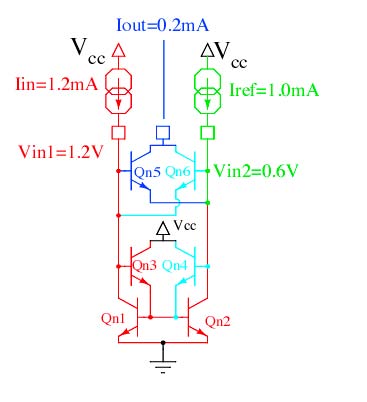
The comparator cell was actually invented as a way to perform 

an absolute value function on two input current sources (4,069,460). 

It has since then found other uses, such as for a precise AM decoder

for use in an AM stereo decoder (4,359,693). 

The circuit is essentially a dual input current mirror in which the larger 

of two input currents take over the current mirror. Some voltage clamping 

transistors prevent saturation while provide an output current 

equal to the absolute difference between the two input currents. 

If Iin is 0.2mA larger than Iref, 1.2mA will flow in Qn1 and Qn2. 

Transistors Qn4 and Qn6 will be off. And transistor Qn5 will make up 

the 0.2mA difference in input current. 

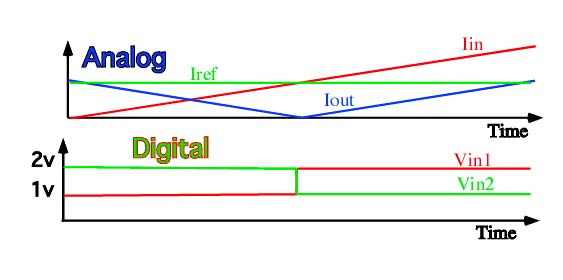
Now if the Iin current is ramping up, it becomes obvious that

the input current is both being compared and folded at the

output at the same time. The comparator's differential input voltage

will toggle around the reference current, and can be used as a 

differential digital output port. The absolute value output current 

happens to be the input current folded around the reference current. 

This folded output current can be sent to another stage, and 

the analog signal gets compared and folded a again. 

The current processing of the signal is mathematical. Each stage

compares the current between an analog input current and a

reference current. The analog input current further gets

folded to an absolute value of the difference between the two

input currents. This folded output current can then be passed 

on to a series of following stages.  

But the folding of the analog signal is being done just like 

it would be done on a piece of paper. Every fold means a 

half reduction in magnitude. This means that the reference currents 

will have to be reduced by a factor of two at each stage. A need

for speed makes it desirable to use minimum geometries for all 

transistors in the signal path. And all the transistors need to operate

at an optimum current level to have a maximum ftau.  

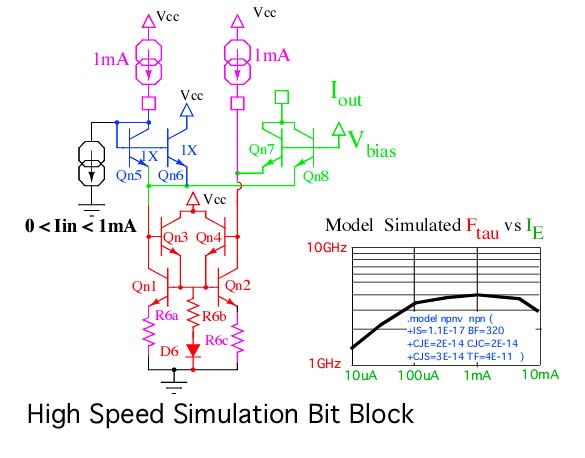
Some simple first order techniques to address speed issues are

shown in the circuit above. Transistors Qn6 and Qn5 make up for

the gain reduction happening at each current fold. A NPN transistor 

which has a 4GHz ftau is being used as a model. This NPN has an 

optimum ftau around 1mA. Transistors Qn1 to Qn4 all want to

be biased up to run as fast as possible. Diode D6 and resistor R6b

are biasing Qn3 and Qn4. Degeneration resistors at Qn1 and Qn2 may be 

desirable to enhance matching. 

The biggest problem is when a transistor turns off, it often 

takes a while to turn back on. So transistors Qn7 and Qn8 have

pick up the additional job of being clamping diodes. The voltages

between the bases of Qn3 and Qn4 is the actual digital output.

These nodes are going to want to go to some differential logic

stage. Raising the Vbias voltage applied to Qn7 and Qn8 

will begin to limit the voltage swing of the differential digital 

output. So Vbias can control the degree to which transistors 

like Qn3, Qn4, Qn7 and Qn8 can turn off.  So how little of a input

voltage does internal differential logic need? A swing around

+/- 50mV between the bases of Qn3 and Qn4 might be a good place 

to start.

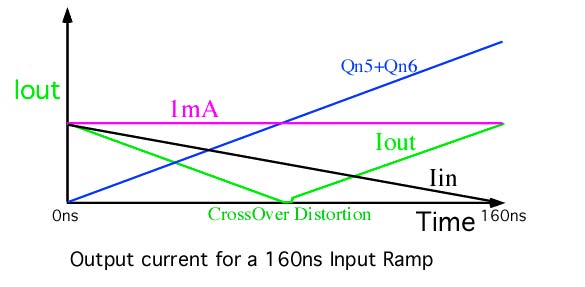
Whenever something turns off, it will have a little delay 

at turning back on. In amplifier applications, this is often

called cross over distortion. It will create a glitch for 

a short amount of time. Biasing transistors to stay on will

reduce this effect.

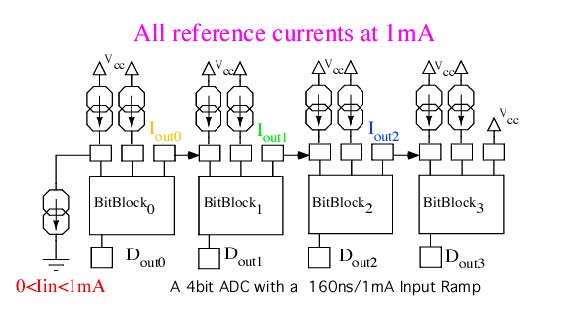
Using the higher speed cells, the connection of the cells

has becomes easier. Everything gets biased to the same reference

current of 1mA. This tends to biases all NPNs at a maximum ftau.

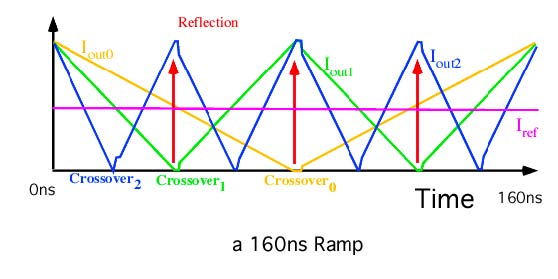
The crossover glitches have a convenient format. They appear

to want to distort all the folded analog waveforms at their

endpoints. This is convenient in that the critical current

comparison is always happening at the center of the folded 

waveforms.

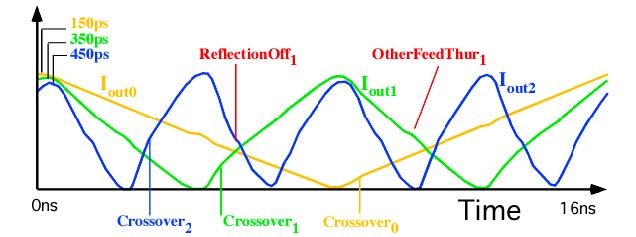
But folding every stage means that currents get toggled

twice as fast for every bit stage. When toggling speeds approach the

ftau of the transistors, the crossover glitches may no longer

be at just the endpoints. At high enough speeds, they begin

to migrate away from the endpoints, and start interfering with 

the current comparison process. 

This is an interesting type of failure. It means that missing 

lsb codes starts to appear at higher input slew rates. So there

is a bit resolution versus input slew rate tradeoff. Put in a

faster moving analog signal, and get a lower bit resolution 

digital output. 

Simulation suggests that 4 cells can track a 16nsec full

scale ramp and produce all 16 individual LSB codes at a rate

of 1GHz per LSB. The ftau for the NPNs is only 4GHz. Only 

some simple speed up techniques were used to do this. Just 

how close the conversion rate can come to matching ftau 

is going to require an exception ability to match silicon 

to spice models. 

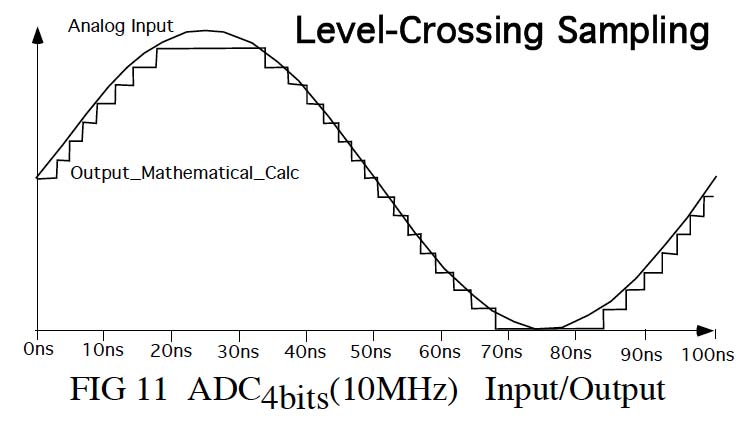
Apply a Full scale 10Mhz sine wave to the input, and then mathematically

reconstruct the digital output back into a analog waveform. This shows

that the output transitions are not happening at a periodic rate. In some

applications, this has the benefit in that the digital output is only

changing state when something is actually happening. 

This kind of digitizing of analog signal has been referred to as

level crossing sampling, or as a threshold crossing detector,

or as an Asynchronous Analog-to-Digital Converters,    

or even as a Level-Crossing Flash Asynchronous Analog-to-Digital Converter. 

Where as a normal A to D stores it resolution in terms of a precise voltage

level, this type of converter stores its resolution in terms of 

a precise time when something has happened. There has been some interest 

in using this type of a converter lately. The following are some recent

examples of Asynchronous ADC activity off the web. 

6 bit Asynchronous December 2006
Asynchronous ADC In CAD Mentor Graphics
Asynchronous Data Processing System
ASYNCHRONOUS PARALLEL RESISTORLESS ADC

LEVEL BASED SAMPLING FOR ENERGY CONSERVATION IN LARGE NETWORKS

A Level-Crossing Flash Asynchronous Analog-to-Digital Converter

Weight functions for signal reconstruction based on level crossings

Adaptive Rate Filtering Technique Based on the Level Crossing Sampling

Adaptive Level–Crossing Sampling Based DSP Systems 

A 0.8 V Asynchronous ADC for Energy Constrained Sensing Applications 

Spline-based signal reconstruction algorithm from multiple level crossing samples

A New Class of Asynchronous Analog-to-Digital Converters

Effects of time quantization and noise in level crossing sampling stabilization

Here is some more background information on Analog to Digital converters.

A 1-GS/s 6-bit 6.7-mW ADC
A Study of Folding and Interpolating ADC

Folding_ADCs_Tutorials5
high speed ADC design
Investigation of a Parallel Resistorless ADC

Here are some patents on the subject.

4,291,299_Analog_to_digital_converter_using_timed

4,352,999_Zero_crossing_comparators_with_threshold
4,544,914_Asynchronously_controllable_successive_approximation
4,558,348_Digital_video_signal_processing_system_using
5,001,364_Threshold_crossing_detector

5,315,284_Asynchronous_digital_threshold_detector_
5,945,934_Tracking_analog_to_digital_converter

6,020,840_Method_and_apparatus_for_representing_waveform
6,492,929_Analogue_to_digital_converter_and_method

6,501,412_Analog_to_digital_converter_including_a_quantizers
6,667,707_Analog_to_digital_converter_with_asynchronous_ability
6,720,901_Interpolation_circuit_having_a_conversio2

6,850,180_SelfTimed_ADC
6,965,338_Cascade_A_D_converter

7,133,791_Two_mean_level_crossing_time_interval

This is a different type of style of ADC. (Event Sampling)

About Folding ADCs
An easy architecture to perform the same function
Folding and Flash architectures have been around for some time
But none this simple.
Level Crossing + Asynchronous ADC follows different rules
AADC sampled with a clock, is normal ADC
Threshold Sampling may look like it is truncating data.
An easy extrapolation method is shown here
More advanced methods are found here.
Extrapolation actually works quite well.
Additional Event Sampling to Threshold Sampling.

11.19.10_1.20PM 

dsauersanjose@aol.com

Don Sauer