Parabola Plotting Web Pages

Thanks to HTML5, graphics is now available on web pages.

Using this feature to design parabolas, is as an

example of what is now available. 

Different applications require parabolas having different

focal points. For convenience, let focal length be define

relative to the parabola's radius. The old camera flash 

bulbs use to use a parabola similar to above. Parabolas

follow the equation below.  

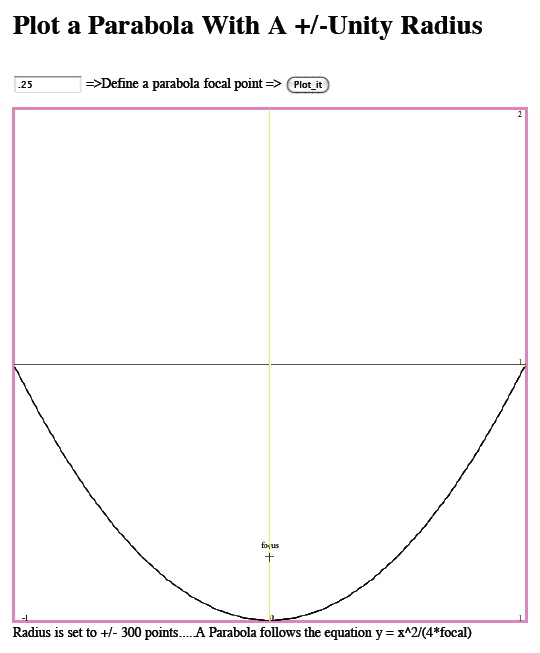
     y = X^2/(4*focal)

When the focal is .25, y will be one when x is one. 

This webpage allows a focal point to be entered

and it will do all the plotting.  

Something like a solar cooker might require a focal

length more like shown below. 

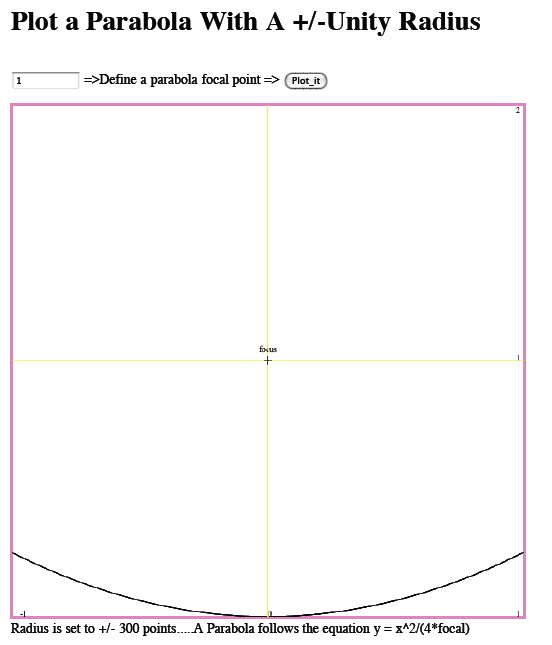
When the focal is 1, y will be 0.25 when x is one. 

So X can be thought of as the radius of the parabola,

and y as being the depth. 

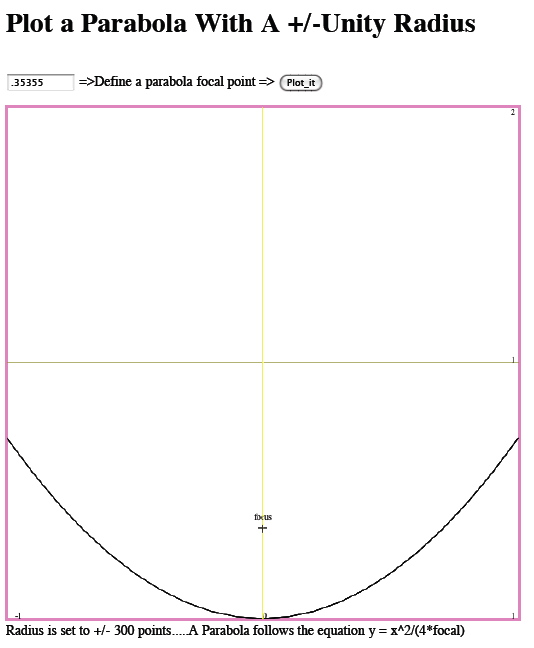
Some applications may want the focal point to be close

to one half the depth. 

Making the focal length equal to sqrt(1/8) will do 

the job.  

This same graphing feature can be extended to a web

page that can actually graph out the segments of 

the parabola.

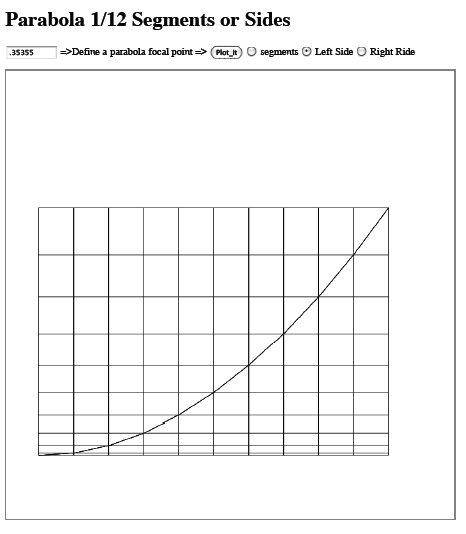
In this webpage, select a focal length and select

whether to plot segments or the parabola sides.  

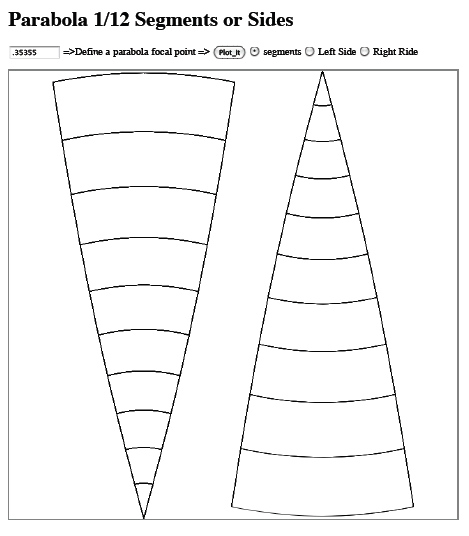
The parabola plots x as being step by 

a consistent amount and the corresponding 

y values displayed as lines.  

The web pages have been designed to be able to 

directly print out the curves on one page. Or 

they can be saved as a pdf file. 

Print out three segments and the left and 

right sides, then construct the parabola. This

will show how well everything lines up. All the 

lines are present for alignment purposes.

The segments have been designed to have a consistent 

spacing in the x direction. The curve of the segments

will align themselves with both the x and y lines

on the left and right sides. 

The web page is plotting everything on a 700x700 canvas.

Things have been simplified for a one page printout. Unlike

most plotting resources, the x and y are not seeing a funny

auto scale. 

The plot is for now a bit map. The plot will define the shape

to a focal length relative to a radius. One could import the

plots into an application to do some size scaling. It should

be possible to build any size and shape of a parabola desired.